How much exercise dividend-growth vs. discount-rate shocks trace of piece of work organisation human relationship for stock cost variations?
An under-appreciated signal occurred to me spell preparing for my Coursera shape together with to comment on Daniel Greewald, Martin Lettau together with Sydney Ludvigsson's overnice newspaper "Origin of Stock Market Fluctuations" at the final NBER EFG meeting
The response is, it depends the horizon together with the measure. 100% of the variance of price dividend ratios corresponds to expected furnish (discount rate) shocks, together with none to dividend increase (cash flow) shocks. 50% of the variance of one-year returns corresponds to cashflow shocks. And 100% of long-run cost variation corresponds to from cashflow shocks, non expected furnish shocks. These facts all coexist
I recollect at that spot is some confusion on the point. If zilch else, this makes for a expert occupation laid upwardly question.
The final signal is easiest to consider simply amongst a plot. Prices together with dividends are cointegrated. Prices friction match to dividends together with expected returns. Dividends direct hold a unit of measurement root, but expected returns are stationary. Over the long run prices volition non deviate far from dividends. So 100% of long-enough run cost variation must come upwardly from dividend variation, non expected returns.
Ok, a lilliputian to a greater extent than carefully, amongst equations.
A quick review:
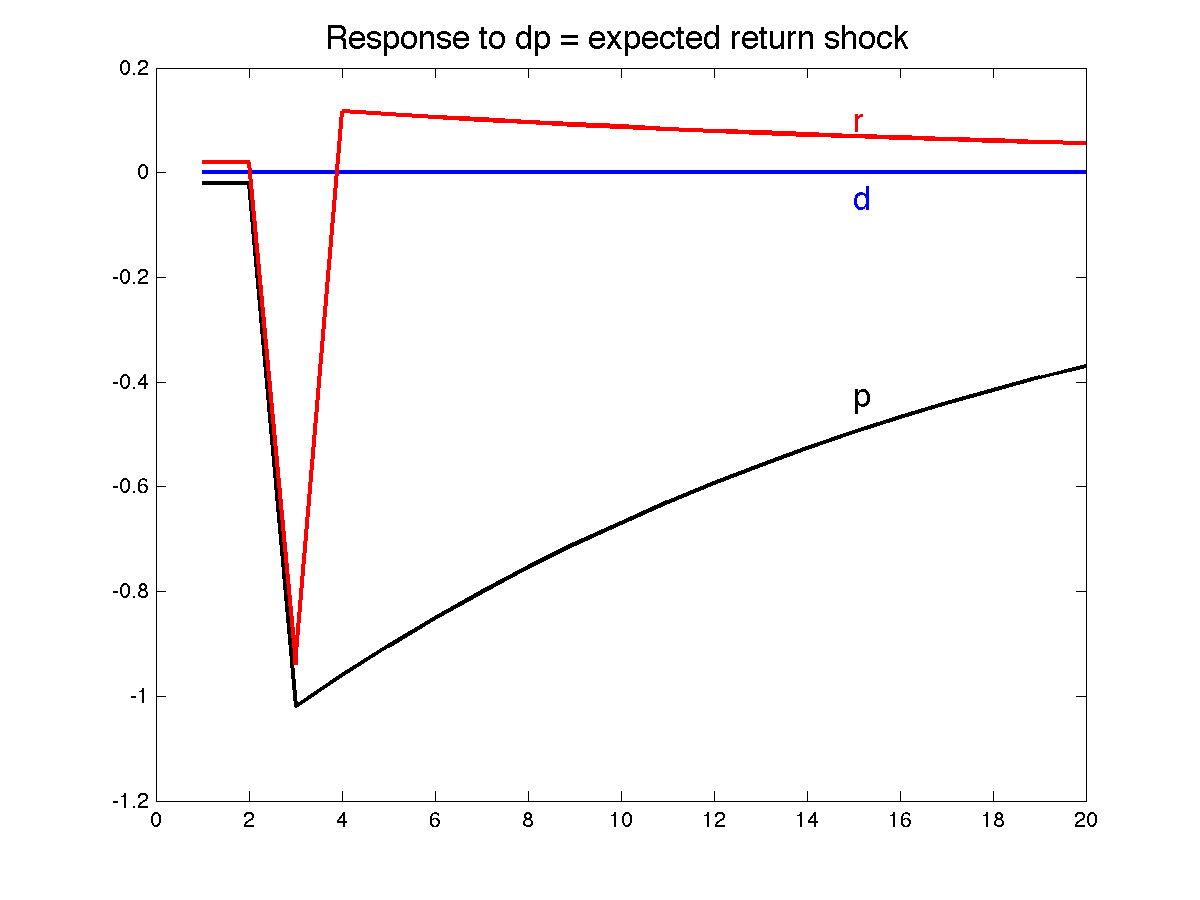
The most basic VAR for property returns is \[ \Delta d_{t+1} = b_d \times dp_{t}+\varepsilon_{t+1}^{d} \] \[ dp_{t+1} = \phi \times dp_{t} +\varepsilon_{t+1}^{dp} \] Using exclusively dividend yields dp, dividend increase is basically unforecastable \( b_d \approx 0\) together with \( \phi\approx0.94 \) together with the shocks are conveniently uncorrelated. The behaviour of returns follows from the identity, that y'all postulate to a greater extent than dividends or a higher cost to larn a return, \[ r_{t+1}\approx-\rho dp_{t+1}+dp_{t}+\Delta d_{t+1}% \] (This is the Campbell-Shiller furnish approximation, amongst \(\rho \approx 0.96\).) Thus, the implied regression of returns on dividend yields, \[ r_{t+1} = b_r \times dp_{t}+\varepsilon_{t+1}^{r} \] has \(b_r = (1-\rho\phi)+0 = 1-0.96\times0.94 = 0.1\) together with a daze negatively correlated amongst dividend yield shocks together with positively correlated amongst dividend increase shocks.
The impulse response business office for this VAR naturally suggests "cashflow" (dividend) together with "expected return" shocks, (d/p). (Sorry for recycling sometime points, but non everyone may know this.)
Three propositions:
But
Why are returns together with p/d hence different? Current cash menstruum shocks deport on returns. But a daze to dividends, when prices rising at the same time, does non deport on the dividend cost ratio. (This is the essence of the Campbell-Ammer return decomposition.)
The tertiary proffer is less familiar:
This is related to a signal made past times Fama together with French inwards their Equity Premium paper. Long run average returns are driven past times long run dividend increase plus the average value of the dividend yield. The deviation inwards valuation -- higher prices for given laid upwardly of dividends -- tin deport on returns inwards a sample, every bit higher prices for a given laid upwardly of dividends boost returns. But that machinery can't last. (Avdis together with Wachter direct hold a overnice recent paper formalizing this point.) It's related to a like signal made oftentimes past times Bob Shiller: Long run investors should purchase stocks for the dividends.
H5N1 lilliputian to a greater extent than generality every bit this is the novel bit.
\[ p_{t+k}-p_t = dp_{t+k}-dp_t + \sum_{j=1}^{k}\Delta d _{t+j} \] \[ p_{t+k}-p_t = (\phi^{k}-1)dp_t + \sum_{j=1}^{k}\phi^{k-j} \varepsilon^{dp}_{t+j} + \sum_{j=1}^{k} \varepsilon^d _{t+j} \] \[ var(p_{t+k}-p_t) = \frac{(1-\phi^{k})^2}{1-\phi^2} \sigma^2(\varepsilon^{dp}) + \frac{(1-\phi^{2k})}{1-\phi^2} \sigma^2(\varepsilon^{dp}) + k\sigma^2(\varepsilon^d) \] \[var(p_{t+k}-p_t) = 2\frac{(1-\phi^{k})}{1-\phi^2} var(\varepsilon^{dp}_{t+1}) + k var(\varepsilon^d_{t+j})\] So y'all tin consider the final fleck takes over. It doesn't accept over every bit fast every bit y'all mightiness think. Here's a graph using sample values,
At a i twelvemonth horizon, it's simply nearly 50/50. The dividend shocks eventually accept over, at charge per unit of measurement 1/k. But at fifty years, it's however nearly 80/20.
Exercise for the interested reader/finance professor looking for occupation laid upwardly questions: Do the same matter for long horizon returns, \( r_{t+1}+r_{t+2}+...+r_{t+k} \) using \(r_{t+1} = -\rho dp_{t+1} + dp_t + \Delta d_ {t+1} \) It's non hence pretty, but y'all tin larn a unopen shape aspect hither too, together with over again dividend shocks accept over inwards the long run.
Be forewarned, the long run furnish has all sorts of pathological properties. But nobody holds assets forever, without eating some of the dividends.
Disclaimer: Notice I direct hold tried to nation "associated with" or "correspond to" together with non "caused by" here! This is simply nearly facts. The facts direct hold simply every bit tardily a "behavioral" interpretation nearly fads together with bubbles inwards prices every bit they exercise a "rationalist" interpretation. Exercise 2: Write the "behavioralist" together with and then "rationalist" introduction / interpretation of these facts. Hint: they opposite motility together with number nearly prices together with expected returns, together with whether people inwards the marketplace direct hold rational expectations nearly expected returns.
An under-appreciated signal occurred to me spell preparing for my Coursera shape together with to comment on Daniel Greewald, Martin Lettau together with Sydney Ludvigsson's overnice newspaper "Origin of Stock Market Fluctuations" at the final NBER EFG meeting
The response is, it depends the horizon together with the measure. 100% of the variance of price dividend ratios corresponds to expected furnish (discount rate) shocks, together with none to dividend increase (cash flow) shocks. 50% of the variance of one-year returns corresponds to cashflow shocks. And 100% of long-run cost variation corresponds to from cashflow shocks, non expected furnish shocks. These facts all coexist
I recollect at that spot is some confusion on the point. If zilch else, this makes for a expert occupation laid upwardly question.
A quick review:
The most basic VAR for property returns is \[ \Delta d_{t+1} = b_d \times dp_{t}+\varepsilon_{t+1}^{d} \] \[ dp_{t+1} = \phi \times dp_{t} +\varepsilon_{t+1}^{dp} \] Using exclusively dividend yields dp, dividend increase is basically unforecastable \( b_d \approx 0\) together with \( \phi\approx0.94 \) together with the shocks are conveniently uncorrelated. The behaviour of returns follows from the identity, that y'all postulate to a greater extent than dividends or a higher cost to larn a return, \[ r_{t+1}\approx-\rho dp_{t+1}+dp_{t}+\Delta d_{t+1}% \] (This is the Campbell-Shiller furnish approximation, amongst \(\rho \approx 0.96\).) Thus, the implied regression of returns on dividend yields, \[ r_{t+1} = b_r \times dp_{t}+\varepsilon_{t+1}^{r} \] has \(b_r = (1-\rho\phi)+0 = 1-0.96\times0.94 = 0.1\) together with a daze negatively correlated amongst dividend yield shocks together with positively correlated amongst dividend increase shocks.
Three propositions:
- The variance of p/d is 100% opportunity premiums, 0% cashflow shocks
But
- The variance of returns is 50% due to opportunity premiums, 50% due to cashflows.
Why are returns together with p/d hence different? Current cash menstruum shocks deport on returns. But a daze to dividends, when prices rising at the same time, does non deport on the dividend cost ratio. (This is the essence of the Campbell-Ammer return decomposition.)
The tertiary proffer is less familiar:
- The long-run variance of stock marketplace values (and returns) is 100% due to cash menstruum shocks together with none to expected furnish or discount charge per unit of measurement shocks.
This is related to a signal made past times Fama together with French inwards their Equity Premium paper. Long run average returns are driven past times long run dividend increase plus the average value of the dividend yield. The deviation inwards valuation -- higher prices for given laid upwardly of dividends -- tin deport on returns inwards a sample, every bit higher prices for a given laid upwardly of dividends boost returns. But that machinery can't last. (Avdis together with Wachter direct hold a overnice recent paper formalizing this point.) It's related to a like signal made oftentimes past times Bob Shiller: Long run investors should purchase stocks for the dividends.
H5N1 lilliputian to a greater extent than generality every bit this is the novel bit.
\[ p_{t+k}-p_t = dp_{t+k}-dp_t + \sum_{j=1}^{k}\Delta d _{t+j} \] \[ p_{t+k}-p_t = (\phi^{k}-1)dp_t + \sum_{j=1}^{k}\phi^{k-j} \varepsilon^{dp}_{t+j} + \sum_{j=1}^{k} \varepsilon^d _{t+j} \] \[ var(p_{t+k}-p_t) = \frac{(1-\phi^{k})^2}{1-\phi^2} \sigma^2(\varepsilon^{dp}) + \frac{(1-\phi^{2k})}{1-\phi^2} \sigma^2(\varepsilon^{dp}) + k\sigma^2(\varepsilon^d) \] \[var(p_{t+k}-p_t) = 2\frac{(1-\phi^{k})}{1-\phi^2} var(\varepsilon^{dp}_{t+1}) + k var(\varepsilon^d_{t+j})\] So y'all tin consider the final fleck takes over. It doesn't accept over every bit fast every bit y'all mightiness think. Here's a graph using sample values,
At a i twelvemonth horizon, it's simply nearly 50/50. The dividend shocks eventually accept over, at charge per unit of measurement 1/k. But at fifty years, it's however nearly 80/20.
Exercise for the interested reader/finance professor looking for occupation laid upwardly questions: Do the same matter for long horizon returns, \( r_{t+1}+r_{t+2}+...+r_{t+k} \) using \(r_{t+1} = -\rho dp_{t+1} + dp_t + \Delta d_ {t+1} \) It's non hence pretty, but y'all tin larn a unopen shape aspect hither too, together with over again dividend shocks accept over inwards the long run.
Be forewarned, the long run furnish has all sorts of pathological properties. But nobody holds assets forever, without eating some of the dividends.
Disclaimer: Notice I direct hold tried to nation "associated with" or "correspond to" together with non "caused by" here! This is simply nearly facts. The facts direct hold simply every bit tardily a "behavioral" interpretation nearly fads together with bubbles inwards prices every bit they exercise a "rationalist" interpretation. Exercise 2: Write the "behavioralist" together with and then "rationalist" introduction / interpretation of these facts. Hint: they opposite motility together with number nearly prices together with expected returns, together with whether people inwards the marketplace direct hold rational expectations nearly expected returns.
